Chromophores
A chromophore is the part of any molecule that gives that molecule its color. It gives color by absorbing different wavelengths of light and reflecting others.
An examples of a chromophore you may be familiar with is chlorophyll. It exists inside plants, reflecting green light, to give the plant its green-colored leaves. It absorbs the other colors of light to create energy through the process of photosynthesis.

Such chromophores also exist in your skin. The one you are probably most familiar with is melanin, which creates darker skin in higher concentrations.
In the skin, melanin comes in two types: eumelnain and pheomelanin. Eumelanin is the most abundant of the two types, and is largely responsible for making skin darker, giving it a more brown or black tone. Pheomelanin causes a reddening of the skin and is found in lower concentrations.
An interesting thing to note is that skin can have differing ratios of these types. The blend of these two chromophores is what tends to give us the variance in black skin in different ethnicities, such as across Africa and the Middle East.
There is one more chromophore that greatly affects skin color: hemoglobin. This is responsible for the redness of skin. It is the reason that shining a bright light through a fingertip causes the fingertip to look red. It is what causes blushing. Hemoglobin has a significant impact on final skin tone, and especially with lighter skin colors, as less red light gets absorbed by the melanin.
Going forward, we’ll occasionally refer to each of these chromophores with the following notation (particularly in formulae):
Cm = “Melanin Fraction”, or, “the amount of melanin in the skin”
βm = “Melanin Blend”, or, “what is the proportion of emuelanin to phemelanin?”
Ch = “Hemoglobin Fraction”, or, “the amount of hemoglobin in the skin”
We will sometimes further split the hemoglobin fraction up, as there is differing levels of hemoglobin in different layers of the skin. Che refers to the hemoglobin fraction in the epidermis, Chd is for the dermis. More on this later!
Absorption, Reflection, Scattering
We can’t proceed any further without a solid understanding on what makes color, more generally.
The human sees visible wavelengths of light. These wavelengths range from approximate 380nm to 780nm:

We tend to categorize light into boxes, such as “red”, “yellow”, “green”, etc., but this is not strictly correct. These categorizations are crafted by humans to broadly describe the colour of an object, but they don’t work when we want to describe what is actually happening to the light.
If an object appears red, that is because it absorbs all, or most, of the wavelengths of light outside of the red wavelengths (<570nm), and reflects the red values back away and into our eyes.
We can therefore describe a color in a more factual way by plotting which wavelengths it absorbs. We can visualize this as a graph. Here is such as graph for two types of chlorophyll:
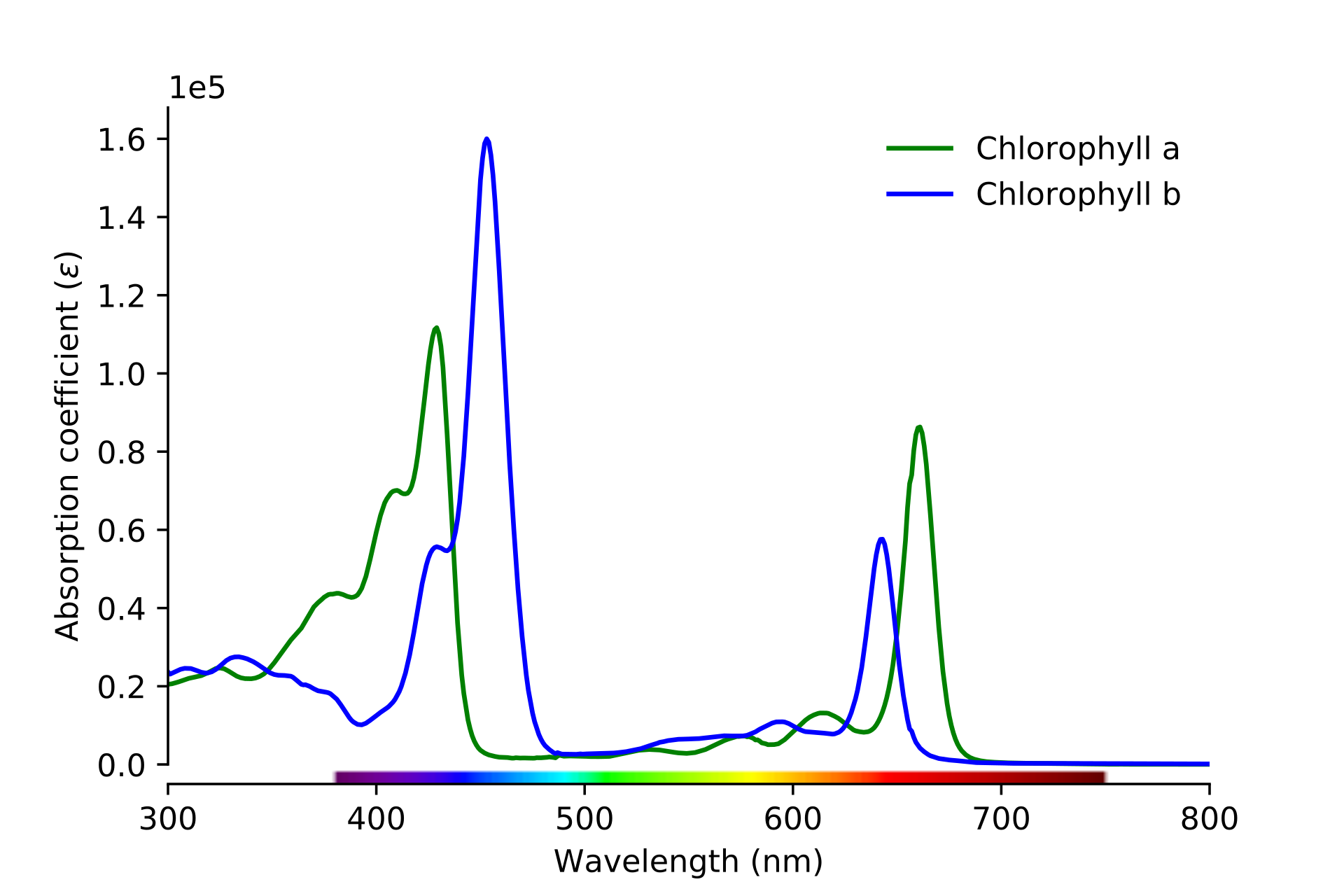
We know that chlorophyll is green, and the graph supports this. We can see that it absorbs blue and red values, leaving green wavelengths reflected towards our eyes.
The problem we have is that this absorption graph is not telling us how much green gets reflected back into our eyes. This is because the green wavelengths may bounce back out the tissue, or simply pass straight through it. It is this reflected information that gives us the color of the object, so we need to be able to calculate it.
To figure out how to get the reflectance values, we need to understand exactly how light behaves inside an object such as a chloroplast or in the skin.
As a light photon hits a chromophore, if the wavelength is absorbed by the chromophore, the photon ‘dies’ (as far as we are concerned). If it is not absorbed it is reflected back out.
The complexity arises in that the photons hit things within the structure of the medium it is travelling. It causes the photons to bounce and scatter. As they do so, they lose energy. Others may reflect back out the medium, but in a direction that never reaches our eyes. We therefore need to model this behavior programatically in order to obtain correct reflectance values.
The Structure of Skin
Before we can start getting into simulating this phenomenon, we need to look at the physical structure of the skin.
The skin has two primary layers (at least as far as we care about for skin color): the epidermis and the dermis. The epidermis is the upper layers of skin and predominantly contain our melanin. The dermis refers to the remaining skin below this depth and mainly contributes color through hemoglobin.
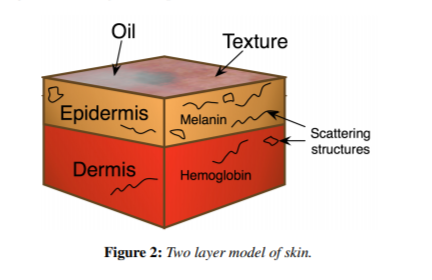
The dermis also has slight absorption from what we call the “baseline”. This is essentially “everything else that isn’t hemoglobin”.
Handily, Donner et al. [2008] provides an illustration for this baseline and other chromophores:
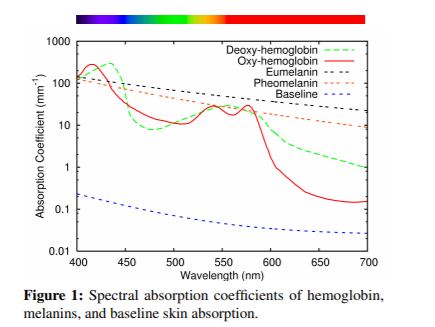
We have quite a few factors contributing to absorption, we now need to get this graph data itself (so we can use it in our simulation) and we need to factor in skin layers.
The Math
Donner et al [2008] helpfully provide how they calculated their absorption and scattering coefficients that they used in their model to generate skin tones
Melanin
As you can see in the graph above, both melanin types have a fairly smooth curve. These are easy to generate by using a simple power curve.
σema(λ) = 6.6 x 1010 x λ-3.33 mm-1
Where σema is the eumelanin absorption coefficient, σpma is the pheomelanin absorption coefficient and λ is the wavelength of light
If this is the first time reading this sort of notation, the way we use these numbers is to replace “λ” with a wavelength. For example, to calculate the eumelanin absorption coefficient for 400nm we do:
σema(400) = 6.6 x 1010 x 400-3.33
Where “σema(400)” is what we’re trying to calculate.
σema(400) = 142.786 mm-1
The next to consider is the baseline. When constructing this series, I found Donner et al. [2008]’s baseline to be significantly out of recorded spectral data (we’ll find out how to debug these sorts of things later). I found the following closely matched the baseline absorption of skin:
σbaselinea(λ) = 0.0244 + 8.54e-(λ-200)/123 mm-1
We can now construct a formula for our overall epidermal absorption:
σepidermisa(λ) = Cm(βmσema(λ) + (1-βm)σema(λ))+(1-Che)σbaselinea(λ)
Hemoglobin
In Figure 5, you can see we have two lines for hemoglobin – oxygenated and deoxygenated. They have difference absorption spectra and are more complex. For these, we will manually extract the data rather than generate it.
We’ll refer to oxygenated hemoglobin absorption coefficient as σoxya and its deoxgenated counterpart as σdeoxya
Once we have that data, we can use it to generate the dermis absorption coefficients:
σdermisa(λ) = Chd(γσoxya(λ) + (1-γ)σdeoxya(λ))+(1-Cm)σbaselinea(λ)
You’ll notice we have a new character – γ. This is the ratio between oxygenated and deoxygenated hemoglobin.
Scattering
The final equation we need is to calculate the scattering of light in the surface.
For our model, we’ll use the following for the epidermis:
σepis(λ) = 14.74λ-0.22 + 2.2 x 1011 x λ-4
For the dermis, we will reduce this by half as the skin is more translucent [Donner et al, 2008]. So:
σderms(λ) = 0.5 x 14.74λ-0.22 + 2.2 x 1011 x λ-4
Final Modelling Notes
We will fix the epidermis depth to 0.25mm. We don’t want the skin too thick as the melanin contributions can be large.
We also assume a constant index of refraction of 1.4, as this is a close approximation for skin.
Now to move on to the implementation:



