<< Go Back Next Page >> NSFW warning for further down this page Let’s take our shader and add in some new features: melanin and hemoglobin masks. Using these masks will enable us to: Add in tan lines (farmers’ tan, swimsuit tans) Mask areas for less melanin pigmentation, such as palms Read more…
<< Go Back Next Page >> Now we need to bring out LUT into a skin shader. For this tutorial, we’ll be using the Bust_Outdoors level from the Digital Human content pack, which you get through the Epic Games Launcher (via Unreal Engine -> Learn). Once you’re there, we’ll move on Read more…
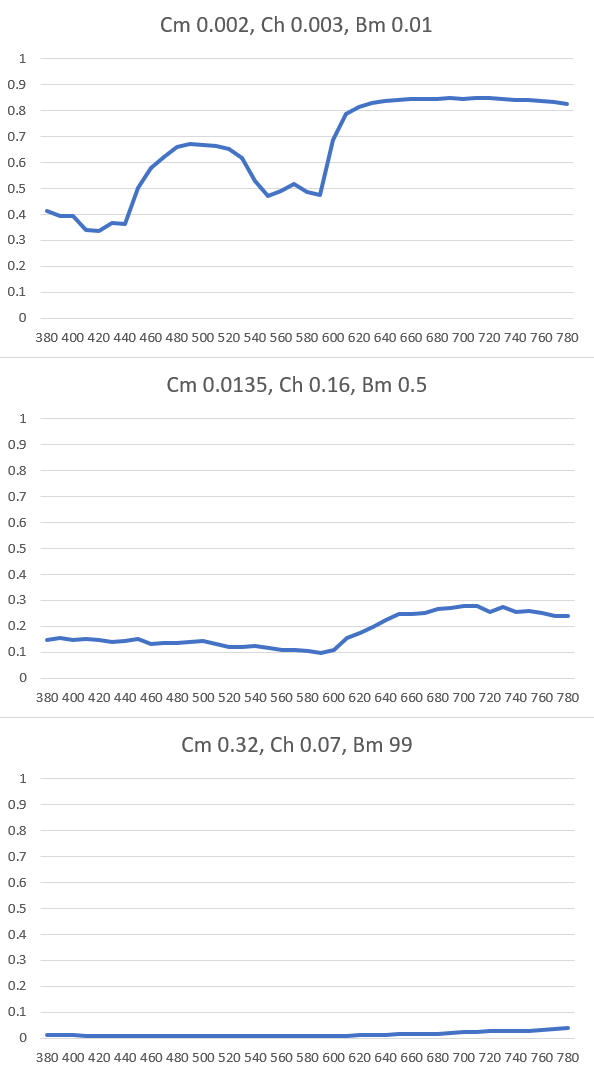
<< Go Back Next Page >> We now need to write out our sRGB values to an image. We installed Pillow in the introduction, so import that now. Below our sRGB conversion loop in the Generate() function If you now run the code you should get this PNG output – its Read more…
<< Go Back Next Page >> XYZ Spectral Sensitivity Curves First, let’s get those Gaussian curves for the XYZ spectral sensitivity curves. I’ve pre-generated these into (you guessed it, CSV). Put this into your development directory, with everything else: In our __init__ function, do the following: And declare at the top Read more…
<< Go Back Next Page >> Having spectral reflectance values is all well-and-good, but this still isn’t a color we can use in a look-up table. Representing Spectral Reflection Values How do we go about converting this data into something usable? Fortunately much of this work has already been done by Read more…
<< Go Back Next Page >> We’ll take what we learned in the previous part and start fleshing out our Monte Carlo (“MC”) simulation. First, let’s import the random and math classes – we’ll need them. In our Python script, we’ll add a new function to our class. We’ll call this Read more…
<< Go Back Next Page >> Introduction As discussed in previous chapters, we need to simulate light photon beams in order to determine the true color of our surface. The “Monte Carlo” simulation provides a method to do this. The name “Monte Carlo” derives from the randomness used in the method; Read more…
<< Go Back Next Page >> Getting Going First things, open Python IDLE 3.8 (64-bit)… and create a new file… Save this file as Skin_Reflectance_Generation.py, or similar. If you have a preferred IDE for authoring Python, feel free to use that. I wanted to keep this tutorial minimal, hence I’m using Read more…
<< Go Back Next Page >> Chromophores A chromophore is the part of any molecule that gives that molecule its color. It gives color by absorbing different wavelengths of light and reflecting others. An examples of a chromophore you may be familiar with is chlorophyll. It exists inside plants, reflecting green Read more…
<< Go Back Next Page >> Getting Python We’re going to use Python for our producing out LUT. The code can be written in any language, if you prefer. Python was just my preference for prototyping the initial work with, and I stuck with it. You’ll need a version of Python Read more…